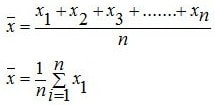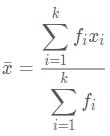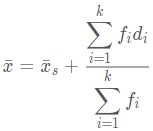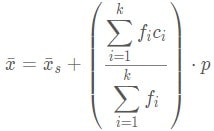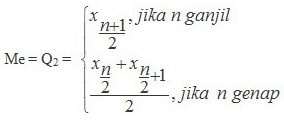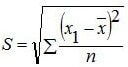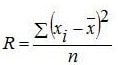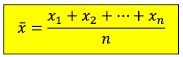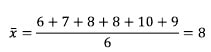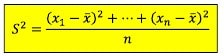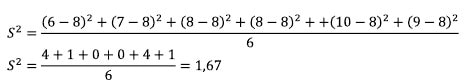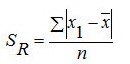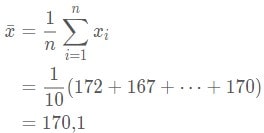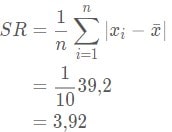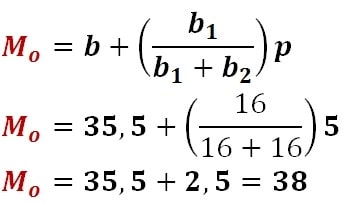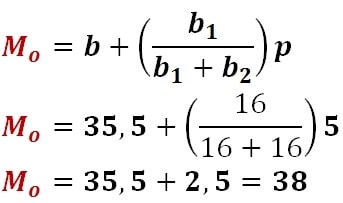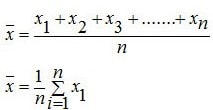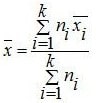Rumus rata-rata Statistika – Statiska adalah ilmu yang mempelajari bagaimana cara membuat rencana, menganalisis, interpretasi, mengumpulkan serta memperesentasikan suatu data. Statististika juga kerap disebut dengan ilmu mengolah data. Sedangkan statistik adalah suatu data saja. Jadi statistika adalah ilmu yang mempelajari tentang analisis data, termasuk, mengumpulkan data, mendiskripsikan serta menyimpulkan data yang ada dengan dasar asumsi teori Probabilitas.
Rumus Statistika merupakan Dasar dalam ilmu matematika dan mulai dipelajari di tingkat Sekolah Menengah Atas (SMA). Lingkup seputar pembelajaran dalam ilmu statistik untuk matematika terdiri dari, mean, median, modus, simpangan, jangkauan serta ragam.
Bagi kalian sekarang masih duduk dibangku SMA harus memahami dan menguasai materi matematika diatas. Apalagi jika kalian ingin bekerja di Badan atau perusahaan dengan dasar ilmu statistik yang kuat. Maka haruslah menguasai mean, modus, median, ragam, simpangan serta jangkauan pada ilmu matematika saat di pelajari di masa SMA.
Rumus rata-rata Statistika data tunggal dan kelompok
Menghitung rata – rata sudah kami bahas pada materi sebelumnya. Apa kamu masih ingat? Nilai rata-rata atau mean adalah cara dalam membagi jumlah nilai data menggunakan banyak data. Rumus rata – rata statistika yakni sebagai berikut:
1. Rumus rata-rata Statistika data tunggal
2. Rumus rata-rata Statistika data kelompok
Untuk menghitung rata-rata data kelompok, terdapat 3 metode untuk kalian pilih.
Pertama, menggunakan titik tengah (cara biasa).
Kedua, menggunakan simpangan rata – rata sementara.
Dimana
Ketiga, memakai pengkodean atau coding
Keterangan:
( ) = rata-rata hitung data berkelompok
s = rata-rata sementara
xi = Nilai tengah kelas ke-i
fi = Frekuensi data kelas ke-i
p = Panjang interval
Ci = kode kelas ke-i
3. Rumus statistika mencari median
Berbicara mengenai median juga telah kami bahas sebelumnya. Rumus statistika median ini merupakan nilai tengah dari suatu data yang belum dikelompokkan. Anda bisa membacanya disini. Sebelumnya, data harus dikelompokkan terlebih dahulu, dimulai dari nilai terkecil ke terbesar secara berurutan.
Jika telah Anda kelompokkan rumus median data nya maka akan seperti berikut ini:
Penjelasannya sebagai berikut:
Rumus Jangkauan Statistika Dasar
Untuk rumus Jangkauan atau rentang Satistika dasar yakni sebagai berikut:
J = xmax – xmin
Keterangan:
xmax = nilai data paling besar
xmin = nilai data paling kecil
Contoh soal:
Berikut ini terdapat data 21,17,19,18,21,19,22,24,26. Carilah jangkauan atau rentang dari data tersebut!
Jawab:
Data terbesar atau xmax yaitu 26.
Data terkecil atau xmin = 17.
Maka rentang / jangkauannya yaitu:
J = xmax – xmin
= 26 – 17
= 9
Rumus Simpangan Quartil Statistika Matematika
Rumus simpangan quartil statistika matematika yaitu:
Qd = 1/2 (Q3– Q1)
Contoh soal:
Perhatikan kuartil dari data berikut ini:
Nilai 4 5 6 8 10
Frekuensi 2 4 7 6 1
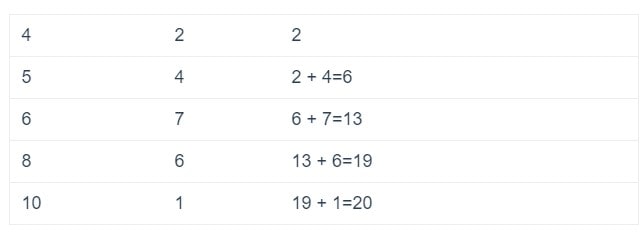
Untuk mencari kuartil, kita cari frekuensi kumulatif juga:
Dari tabel tersebut menurut frekuensi kumulatif dimana:
Disini, n = 20 dan merupakan bilangan genap, oleh karena itu:
Maka, simpangan kuartil dari data tersebut adalah:
= ½ (Q₃ – Q₁)
= ½ (8 – 5)
= ½ (3)
= 1,5
Maka simpangan kuartilnya adalah 1,5.
Rumus Simpangan Baku Statistika Dasar
Contoh soal:
Terdapat data tinggi badan pada sebuah instansi kantor sebagai berikut:
Jawab:
Dari data tabel tersebut, jumlah data (n) = 10 serta (n-1) = 9
Rumus Ragam Statistika Matematika
Contoh soal:
Terdapat suatu deretan angka seperti berikut ini:
6, 7, 8, 8, 10, 9
Carilah ragam (variansi) dari data tersebut!
Jawab:
Langkah pertama adalah mencari rata – rata terlebih dahulu.
Maka nilai rata – ratanya yaitu:
Untuk mencari ragam (variansi):
Maka:
Rumus Simpangan Rata-rata Statistika
Contoh soal:
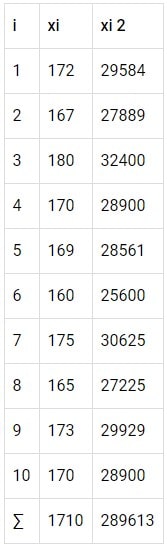
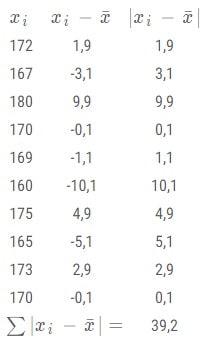
Terdapat data tinggi badan 10 mahasiswa pada salah satu universitas di Yogyakarta. Data tinggi badan adalah sebagai berikut:
Carilah simpangan rata rata statistika dari data tinggi badan tersebut!
Jawab:
Pertama-tama, carilah rata-ratanya:
Lalu hitunglah ∣xi−∣
Lalu kalian dapat menghitung simpangan rata-rata memakai cara berikut ini:
Maka kalian dapatkan hasil perhitungan simpangan rata-rata data tinggi badan diatas adalah 3,92.
4. Rumus statistika dasar menghitung Modus
Rumus menghitung modus terbagi menjadi 2 metode.
Yang pertama, data belum kita kelompokkan, yang mana memiliki frekuensi tertinggi dan dilambangkan dengan Mo
Keterangan:
Mo = Modus serta I merupakan interval kelas
L = tepi bawah dari kelas dimana mempunyai frekuensi tertinggi (kelas modus)
b1 = Frekuensi kelas modus – frekuensi kelas interval terdekat sebelumnya
b2 = Frekuensi kelas modus – frekuensi kelas interval terdekat sesudahnya
Contoh soal:
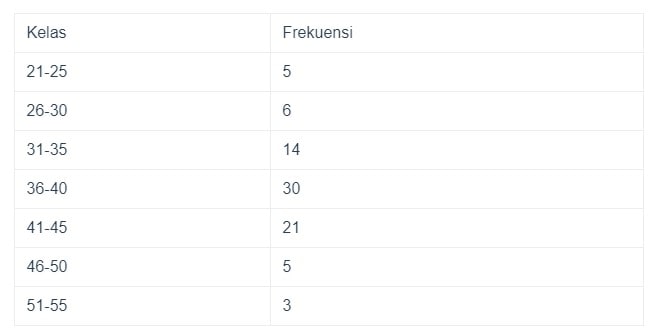
Terdapat tabel frekuensi berikut:
Bila kalian amati tabel diatas, kelas modus ada di rentang 36 – 40. Sebab frekuensinya paling banyak yaitu 30.
Tepi bawah kelas modus bisa kamu cari dengan langkah mengurangi angka terkecil di kelas modus dengan 0,5.
Selanjutnya, tepi bawah = 36 – 0,5 = 35,5.
Disini kamu dapatkan datanya:
b (tepi bawah) yakni 35,5
b1 = 30 – 14 = 16
b2 = 21 – 5 = 16
Panjang kelas adalah 5
Selanjutnya kalian masukkan ke rumus:
Maka didapatkan hasilnya yakni 38.
5. Rumus statistika mencari rata-rata
Mengenai rata-rata atau mean ini sudah kami jelaskan di panduan artikel sebelumnya. Mean adalah nilai rata – rata hitung dengan membagi jumlah nilai dengan banyaknya data yang ada. Terdapat 3 rumus untuk menghitung mean yaitu:
a. Rumus mean data tunggal
b. Rumus mean data dalam distribusi frekuensi
c. Rumus mean hitung gabungan
Untuk penjelasan mengenai mean ini, Anda bisa membaca di artikel cara menghitung mean terutama dengan menggunakan aplikasi Excel.
Demikian pembahasan mengenai rumus rata-rata Statistika data tunggal dan data kelompok kami berharap Anda jelas dalam memahaminya. Pembahasan mengenai rumus rata-rata Statistika data kelompok dan tunggal diatas merupakan rumus dasar yang dipelajari di tingkat SMP dan SMA. Ini sebagai dasar kalian yang tertarik dalam mempelajari limu statistika.

Menyukai dunia traveling, blogging, menulis di blog sejak 2014 sampai sekarang.